Introduzione al Teorema di Bayes
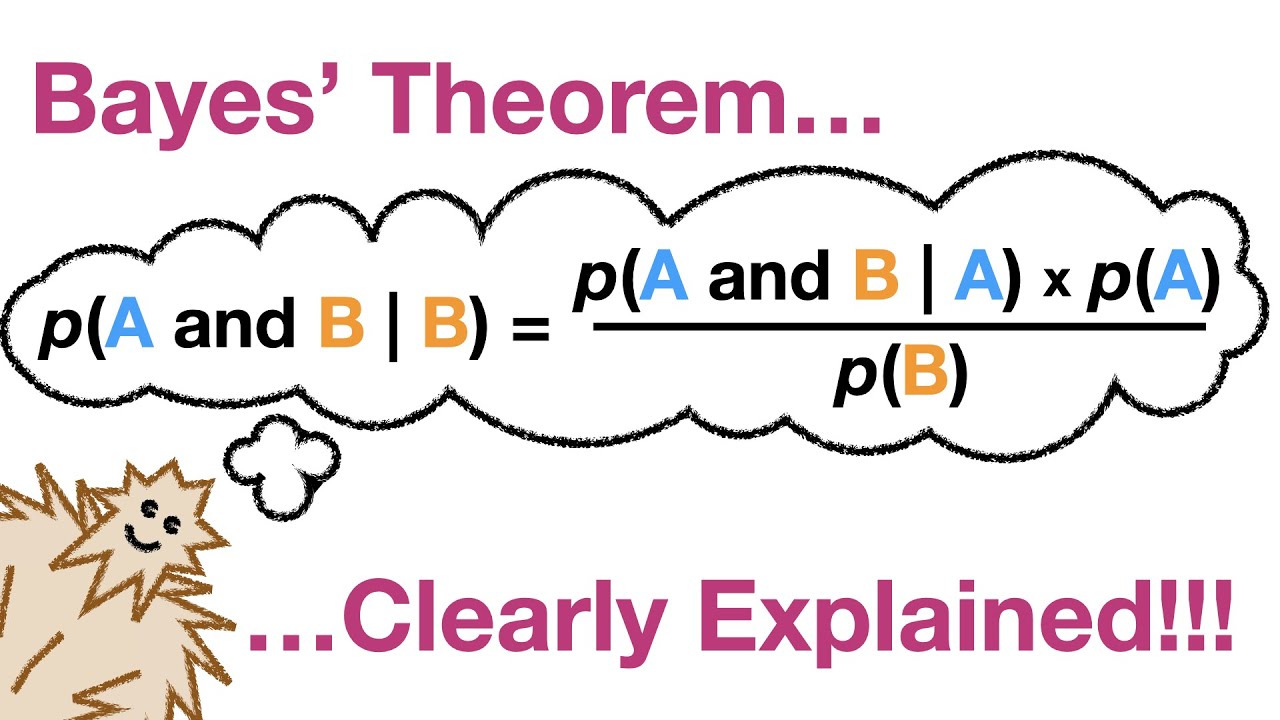
Immagina di avere un test per una malattia rara. Il test è abbastanza preciso, ma non perfetto. Se il test risulta positivo, quanto è probabile che tu abbia davvero la malattia? Il Teorema di Bayes è un potente strumento che ci aiuta a rispondere a questo tipo di domande, fornendoci un modo per aggiornare le nostre credenze sulla base di nuove informazioni.
Il Teorema di Bayes è un’equazione matematica che ci permette di calcolare la probabilità di un evento, dato che si è verificato un altro evento. In altre parole, ci aiuta a capire come la conoscenza di un evento influenza la probabilità di un altro evento.
Applicazione del Teorema di Bayes nella Probabilità Condizionata
Il Teorema di Bayes è strettamente legato al concetto di probabilità condizionata. La probabilità condizionata è la probabilità che un evento si verifichi, dato che un altro evento si è già verificato. Ad esempio, la probabilità che tu abbia la malattia, dato che il test è risultato positivo, è una probabilità condizionata.
Il Teorema di Bayes ci fornisce una formula per calcolare la probabilità condizionata. La formula è la seguente:
P(A|B) = [P(B|A) * P(A)] / P(B)
Dove:
* P(A|B) è la probabilità di A dato B (la probabilità condizionata)
* P(B|A) è la probabilità di B dato A
* P(A) è la probabilità a priori di A
* P(B) è la probabilità a priori di B
Probabilità a Priori e a Posteriori
Nel contesto del Teorema di Bayes, la probabilità a priori è la probabilità di un evento prima di avere nuove informazioni. Ad esempio, la probabilità che tu abbia la malattia prima di fare il test è la probabilità a priori.
La probabilità a posteriori, invece, è la probabilità di un evento dopo aver ricevuto nuove informazioni. Ad esempio, la probabilità che tu abbia la malattia dopo che il test è risultato positivo è la probabilità a posteriori.
Esempi Concreti di Applicazione del Teorema di Bayes
Il Teorema di Bayes ha un’ampia gamma di applicazioni in diversi campi, tra cui:
* Medicina: per diagnosticare malattie, valutare l’efficacia dei trattamenti e prevedere il rischio di complicazioni.
* Finanza: per prevedere il rischio di investimento, valutare il credito e gestire i portafogli.
* Marketing: per personalizzare le campagne pubblicitarie, segmentare i clienti e prevedere il comportamento d’acquisto.
* Scienza forense: per analizzare le prove e determinare la probabilità che un sospettato sia colpevole.
Esempio 1: Immagina di avere un test per il cancro al seno con un tasso di falsi positivi del 5%. Ciò significa che il 5% delle donne sane otterrà un risultato positivo al test. Se il test di una donna risulta positivo, qual è la probabilità che abbia effettivamente il cancro al seno?
Per rispondere a questa domanda, possiamo usare il Teorema di Bayes. Supponiamo che la probabilità a priori di avere il cancro al seno sia dello 0,5% (cioè 1 donna su 200 ha il cancro al seno).
Applicando il Teorema di Bayes, otteniamo:
P(Cancro|Positivo) = [P(Positivo|Cancro) * P(Cancro)] / P(Positivo)
Sapendo che P(Positivo|Cancro) = 1 (se hai il cancro, il test sarà positivo), P(Cancro) = 0,005 e P(Positivo) = 0,05 (il tasso di falsi positivi), possiamo calcolare:
P(Cancro|Positivo) = (1 * 0,005) / 0,05 = 0,1
Questo significa che la probabilità che una donna abbia effettivamente il cancro al seno, dato che il test è risultato positivo, è solo del 10%.
Esempio 2: Immagina di avere un sistema di riconoscimento facciale che ha un tasso di falsi positivi del 1%. Ciò significa che il 1% delle persone che non sono nel database del sistema verrà identificato erroneamente. Se il sistema identifica una persona come sospettato, qual è la probabilità che sia effettivamente la persona cercata?
Per rispondere a questa domanda, possiamo usare il Teorema di Bayes. Supponiamo che la probabilità a priori che la persona sia la persona cercata sia dello 0,01% (cioè 1 persona su 10.000 è la persona cercata).
Applicando il Teorema di Bayes, otteniamo:
P(Sospettato|Cercato) = [P(Cercato|Sospettato) * P(Cercato)] / P(Sospettato)
Sapendo che P(Cercato|Sospettato) = 1 (se la persona è quella cercata, il sistema la identificherà correttamente), P(Cercato) = 0,0001 e P(Sospettato) = 0,01 (il tasso di falsi positivi), possiamo calcolare:
P(Sospettato|Cercato) = (1 * 0,0001) / 0,01 = 0,01
Questo significa che la probabilità che la persona identificata dal sistema sia effettivamente la persona cercata è solo dell’1%.
Applicazioni del Teorema di Bayes: Bayesian

Il Teorema di Bayes, con la sua eleganza e potenza, non è solo un concetto astratto della teoria della probabilità, ma un potente strumento che trova applicazione in un’ampia varietà di campi. Dall’analisi medica alla finanza, dall’intelligenza artificiale all’analisi dei dati, il Teorema di Bayes si dimostra un alleato prezioso per comprendere e gestire l’incertezza, fornendo una base logica per l’aggiornamento delle nostre convinzioni alla luce di nuove evidenze.
Applicazioni del Teorema di Bayes in Diversi Campi
La versatilità del Teorema di Bayes lo rende uno strumento prezioso in diversi campi, permettendo di affrontare problemi complessi e di prendere decisioni informate.
- Medicina: In ambito medico, il Teorema di Bayes è utilizzato per diagnosticare malattie e valutare l’efficacia dei trattamenti. Ad esempio, se un paziente presenta sintomi specifici, il medico può utilizzare il Teorema di Bayes per calcolare la probabilità che il paziente abbia una particolare malattia, tenendo conto della prevalenza della malattia nella popolazione e della sensibilità e specificità del test diagnostico utilizzato.
- Finanza: Il Teorema di Bayes è impiegato nella gestione del rischio finanziario e nella previsione dei prezzi delle azioni. Gli analisti finanziari utilizzano il teorema per aggiornare le loro stime sui rendimenti futuri delle azioni, tenendo conto di nuove informazioni come i risultati aziendali o i cambiamenti macroeconomici.
- Intelligenza Artificiale: Nel campo dell’intelligenza artificiale, il Teorema di Bayes è alla base di molti algoritmi di apprendimento automatico, come i filtri Bayesiani e le reti Bayesiane. Questi algoritmi vengono utilizzati per classificare dati, prevedere eventi futuri e costruire sistemi di intelligenza artificiale che possono apprendere dall’esperienza.
- Analisi dei Dati: Il Teorema di Bayes è uno strumento fondamentale per l’analisi dei dati, permettendo di identificare modelli e relazioni nascoste nei dati. Ad esempio, in ambito marketing, il teorema può essere utilizzato per prevedere la probabilità che un cliente acquisti un determinato prodotto, tenendo conto del suo comportamento di acquisto passato e delle caratteristiche demografiche.
Vantaggi e Svantaggi dell’Utilizzo del Teorema di Bayes, Bayesian
Come ogni strumento, l’utilizzo del Teorema di Bayes presenta sia vantaggi che svantaggi.
- Vantaggi:
- Approccio Logico: Il Teorema di Bayes offre un approccio logico e rigoroso per aggiornare le nostre convinzioni alla luce di nuove evidenze.
- Gestione dell’Incertezza: Il teorema fornisce un modo per quantificare l’incertezza e per aggiornarla in modo sistematico, permettendo di prendere decisioni più informate in situazioni di incertezza.
- Versatilità: Il Teorema di Bayes è applicabile a una vasta gamma di problemi, rendendolo uno strumento versatile in diversi campi.
- Svantaggi:
- Dipendenza dalle Probabilità Precedenti: Il Teorema di Bayes è sensibile alla scelta delle probabilità precedenti, che possono essere difficili da stimare in alcuni casi.
- Calcoli Complessi: I calcoli necessari per applicare il Teorema di Bayes possono essere complessi, soprattutto quando si ha a che fare con un gran numero di variabili.
- Dati Incompleti o Errati: Il teorema può fornire risultati imprecisi se i dati utilizzati sono incompleti o errati.
Riepilogo delle Applicazioni del Teorema di Bayes
La tabella seguente riassume le diverse applicazioni del Teorema di Bayes, includendo i campi di applicazione, i vantaggi e gli svantaggi.
| Campo di Applicazione | Vantaggi | Svantaggi |
|---|---|---|
| Medicina | Diagnosi precisa, valutazione dell’efficacia dei trattamenti | Dipendenza dalle probabilità precedenti, calcoli complessi |
| Finanza | Gestione del rischio finanziario, previsione dei prezzi delle azioni | Dipendenza dalle probabilità precedenti, calcoli complessi |
| Intelligenza Artificiale | Classificazione dei dati, previsione degli eventi futuri, apprendimento automatico | Dipendenza dalle probabilità precedenti, calcoli complessi |
| Analisi dei Dati | Identificazione di modelli e relazioni nascoste nei dati | Dipendenza dalle probabilità precedenti, calcoli complessi |
Approfondimenti sul Teorema di Bayes

Preparati ad immergerti nel cuore del Teorema di Bayes, svelando le sue intricate connessioni con i concetti chiave della probabilità. Attraverso un’esplorazione dettagliata, scoprirai come questo potente strumento analitico consente di aggiornare le nostre credenze alla luce di nuove informazioni.
Probabilità condizionata, probabilità a priori e probabilità a posteriori
La probabilità condizionata, la probabilità a priori e la probabilità a posteriori sono concetti fondamentali che costituiscono il nucleo del Teorema di Bayes.
La probabilità condizionata rappresenta la probabilità che un evento si verifichi dato che un altro evento è già accaduto. Ad esempio, qual è la probabilità che una persona abbia la febbre, sapendo che ha un raffreddore? Questa è una probabilità condizionata.
La probabilità a priori è la probabilità di un evento prima di osservare qualsiasi evidenza. Nel nostro esempio precedente, la probabilità a priori sarebbe la probabilità che una persona abbia la febbre, senza conoscere se ha un raffreddore o meno.
La probabilità a posteriori è la probabilità di un evento dopo aver osservato nuove informazioni. Nel nostro esempio, la probabilità a posteriori sarebbe la probabilità che una persona abbia la febbre, sapendo che ha un raffreddore.
Il Teorema di Bayes fornisce una formula per calcolare la probabilità a posteriori, utilizzando la probabilità a priori, la probabilità condizionata e la probabilità marginale.
Tipi di distribuzioni di probabilità
Le distribuzioni di probabilità descrivono la probabilità di ogni possibile risultato di un evento casuale. Esistono diversi tipi di distribuzioni di probabilità, ciascuna con le sue caratteristiche uniche.
- La distribuzione Bernoulli è una distribuzione discreta che descrive la probabilità di successo o fallimento di un singolo evento. Ad esempio, il lancio di una moneta può essere modellato con una distribuzione Bernoulli, dove il successo è ottenere testa e il fallimento è ottenere croce.
- La distribuzione binomiale è una distribuzione discreta che descrive la probabilità di ottenere un certo numero di successi in una serie di prove indipendenti. Ad esempio, la probabilità di ottenere esattamente 3 teste in 5 lanci di una moneta può essere calcolata usando la distribuzione binomiale.
- La distribuzione normale è una distribuzione continua che è spesso usata per modellare eventi casuali che si distribuiscono in modo simmetrico attorno a un valore medio. Ad esempio, l’altezza degli individui può essere approssimata da una distribuzione normale.
- La distribuzione esponenziale è una distribuzione continua che descrive la probabilità che un evento si verifichi dopo un certo tempo. Ad esempio, la durata di una lampadina può essere modellata con una distribuzione esponenziale.
Il Teorema di Bayes può essere utilizzato con qualsiasi tipo di distribuzione di probabilità. Ad esempio, possiamo usare il Teorema di Bayes per aggiornare la nostra credenza sulla probabilità che una persona abbia una malattia, dato che ha mostrato alcuni sintomi.
Ruolo della probabilità marginale
La probabilità marginale è la probabilità di un evento, senza considerare altri eventi. Nel contesto del Teorema di Bayes, la probabilità marginale è usata per calcolare la probabilità a posteriori.
La probabilità a posteriori è proporzionale alla probabilità a priori moltiplicata per la probabilità condizionata, divisa per la probabilità marginale.
La probabilità marginale rappresenta la probabilità totale di osservare l’evidenza, indipendentemente dal fatto che l’evento sia vero o falso.
Aggiornamento delle credenze con il Teorema di Bayes
Il Teorema di Bayes è uno strumento potente per aggiornare le nostre credenze alla luce di nuove informazioni. In altre parole, ci permette di rivalutare la probabilità di un evento dopo aver osservato nuovi dati.
Ad esempio, supponiamo di voler valutare la probabilità che una persona abbia una malattia, dato che ha mostrato alcuni sintomi. Possiamo usare il Teorema di Bayes per aggiornare la nostra credenza sulla probabilità di malattia, utilizzando la probabilità a priori (la probabilità di malattia prima di osservare i sintomi), la probabilità condizionata (la probabilità di avere i sintomi dato che si ha la malattia) e la probabilità marginale (la probabilità di avere i sintomi, indipendentemente dalla malattia).
Il Teorema di Bayes ci consente di combinare la nostra conoscenza preesistente (probabilità a priori) con nuove informazioni (probabilità condizionata) per ottenere una stima più accurata della probabilità di un evento (probabilità a posteriori).
Bayesian statistics, it’s like a detective trying to figure out whodunnit, but instead of fingerprints, it’s data. You start with a guess, update it with evidence, and then you’ve got your answer. Of course, you need a little bit of autonomy to make those decisions, right?
Just like the detective needs to be able to follow their instincts. Autonomy is crucial for that kind of independent thinking, which is essential in Bayesian analysis. So, next time you’re trying to figure out the odds of something happening, remember, a little bit of autonomy goes a long way in the world of Bayesian statistics!
So you’re telling me you can use Bayesian statistics to predict the weather? That’s like, way more useful than predicting what kind of cheese the captain will order for the crew. Wait, hold on, what’s this about a Bayesian yacht ?
Is that a thing? Sounds like a party I’d want to be at. Anyway, back to the weather… Bayesian methods can really help you navigate those uncertain seas, both literally and figuratively.
